Measuring Diameters & Distances
3.3 - Understand how Eratosthenes and Aristarchus used observations of the Moon and Sun to determine successively:a) diameter of the Earth
b) diameter of the Moon
c) distance to the Moon
d) distance to the Sun
e) diameter of the Sun
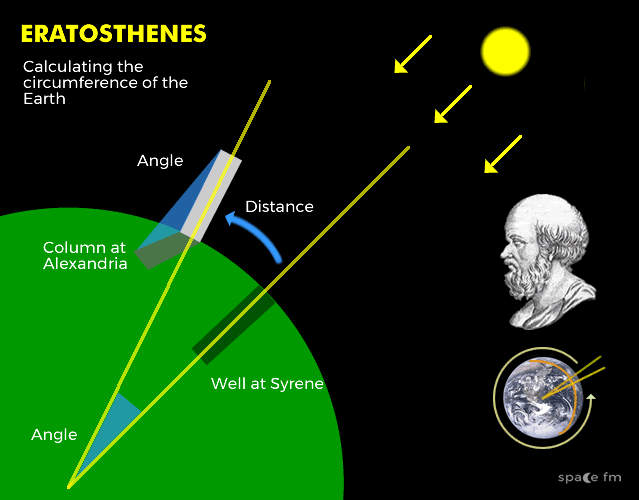
Eratosthenes of Cyrene and the circumference of the Earth
Eratosthenes was a Greek mathematician and was the librarian of Alexandria in Egypt.
He learnt that near the town of Syene (named Aswan today), to the south, the Sun appears at the zenith (the highest point in the sky) on the summer solstice. it was well known that its reflection on this day could be seen directly down a deep well.
By observing and measuring shadows on the same day in Alexandra, he calculated that the Sun was over 7.12° from the Zenith on the same date. This is approximately 1/50th of a circle.
The distance between the cities was approximately 5000 stadia (back then they measured by stadia – like football pitches are used to quickly illustrate lengths).
Eratosthenes made a calculation by multiplying the distance by the angle. He was able to determine the Earth's circumference and then another calculation to work out the diameter.
Confusingly, there were 2 different measurements for a stadia but scientists believe he used a unit which led to the circumference being within 1 degree of the modern known value.
This is even more remarkable as the town he used as his measurement was not directly to the south and was not exactly on the Tropic of Cancer. As if that wasn’t enough, he also invented the word 'Geography'.
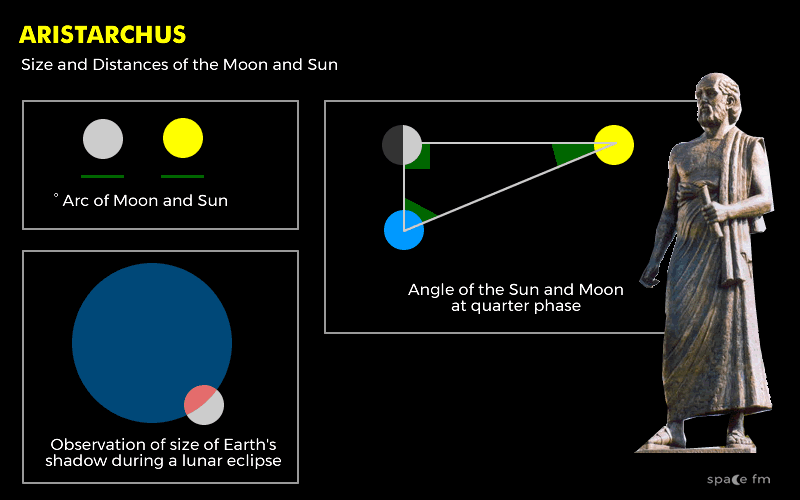
Aristarchus of Samos and the diameters of the Moon, Sun and their distances
Aristarchus was a Greek astronomer who lived at the same time as Eratosthenes and first proposed the idea that the Earth orbited the Sun.
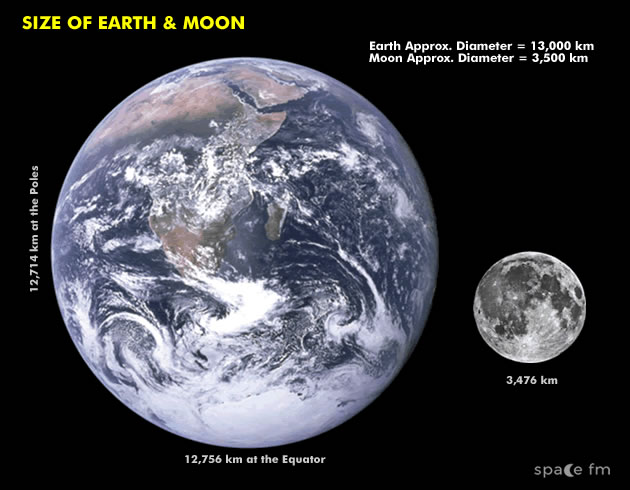
A lunar eclipse allowed him to study the shadow of Earth over the Moon and determined that Earth was twice the size of the Moon
He then measured the width of both Sun and Moon and determined they were 2° of arc in width.
To understand the distances involved, he attempted to triangulate the Moon, Sun and Earth. He measured the angle between a quarter phase moon (what we call a half moon) and the Sun. He found the angle to be 87° and using the mathematics known at the time he derived the Sun was between 18 to 20 times further away than moon.
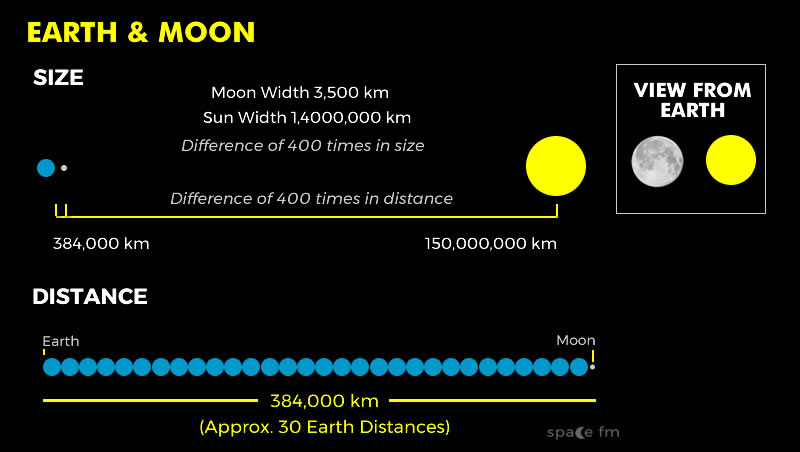
Today we know Earth is four times larger than the Sun today and Sun and Moon are ½° of arc but it was the best measurement of its time. We also now know the angle between a quarter phase moon and the Sun is 89.5° which makes the Sun 400 times further than the Moon but he was accurate in understanding that there was the same ratio between distance and size. The reasoning behind his measurements was good. There were several reasons to explain why his measurements were inaccurate. He wouldn't have had the most advanced scientific instruments to measure angles. Knowing the approximate time when a quarter moon is exactly at 50% illumination is very difficult to ascertain. He may also not have access to knowledge about using the mathematical sine function or advanced trigonometry knowledge that may have improved his estimation.
Links
- Famous Scientists Eratosthenes
- University of St Andrews Aristarchus of Samos
 | © All Rights Reserved |
| © All Rights Reserved |