Gravity and the Inverse Square Law
8.3 - Understand the role of gravity in creating stable elliptical orbits8.7 - Understand that the constant in Kepler’s third law depends inversely on the mass of the central body
8.8 - Know that Newton was able to explain Kepler’s laws using his law of universal gravitation
8.9 - Understand that the gravitational force between two bodies is proportional to the product of their masses and inversely proportional to the square of their separation (algebraic expression of Newton’s law of universal gravitation not required)
13.9 - Understand the inverse square relationship between distance and brightness/intensity
Isaac Newton is known for formulating his thinking of gravity when struck by an apple falling from a tree. The force that made the apple fall was the same force that kept the Moon going around the Earth. The Moon doesn't fall to Earth because it is moving at a velocity greater than the pull of the Earth, but not fast enough to escape Earth’s influence. If the Earth disappeared it would move in a straight line until it was disturbed by another body.
Newton knew that if you fired a cannonball off a cliff it would eventually fall to Earth but if it was fast enough it would continue on and on travelling through the sky and orbit the Earth.
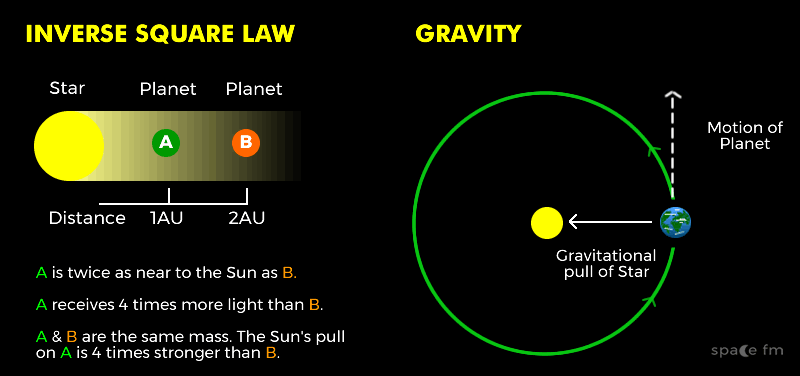
Gravity is the force responsible for creating stable elliptical orbits due to the constant gravitational force between the object and the Sun to keep them in orbit.
The two things that control gravity are mass and distance. The further away you are from the centre of Earth, the weaker the gravity of Earth. You would weigh less on the Moon than the Earth because it has a lot less mass than Earth.
Inverse Square Law
Newton proposed the Inverse Square Law. The effect of gravity (and also on forces such as sunlight) works like this.
If say we have a half-mass Earth, it would produce a gravity of not half but a quarter (the square of 2). If Earth was three times closer to the Sun it would get not 3 times as much light but 9 times as much (the square of 3 is 9).
If we have two bodies of a different mass at a distance from each other we can calculate the gravitation force. And for that we need some sums from Mr Newton.
Relation to Kepler’s Laws
Kepler showed how planets move, Newton was interested in the movement itself rather than the object – for every action there is an equal and opposite reaction. As an object orbits nearer another in an elliptical orbit there must be an increase in gravitational force between them at that point.When looking Kepler’s third law (the relationship between distance and time of orbit) Newton proposed the force is proportional to the sum of the masses of both objects. It inversely relies on the mass of the Sun essentially.
The Sun has gravitational influence on Earth but the opposite is also true so the Sun and Earth’s mass should be used to calculate the gravitational force between them. The amount of difference is small because the Sun is so large but it is more accurate than Kepler’s.
A Calculation
Here is an example by James E. Heath from Austin Community College.
We've previously used:
T = Period/ Time it takes to orbit the Sun
r = mean radius from Sun
In this example P is Period (T) and A is axis rather than radius (r) but it's the same thing.
Consider two stars, one of 10 solar masses and another of 6 solar masses, in a binary system. It takes one star 2 years to orbit the common centre of mass. What is the semi-major axis of this star's orbit?
M1 = 10 solar masses
M2 = 6 solar masses
P = 2 years
A = ?
We need to use Newton's Version of Kepler's Third Law for this problem. Start with the basic equation and rearrange it to solve for A:
M1 + M2 = A3 / P2
A3 = (M1 + M2) x P2
A3 = (10 + 6) x (2)2 = 16 x 4 = 64
Take the cube root of 64 to get 4, and the two stars are 4 Astronomical Units apart.
Questions
Questions involving the Inverse Square Law will ask you to compare values such as light or gravity and ask you to make a calculation based on the Inverse Square Law.
Question 1
Planet A lies at 2 AU from the Sun. Planet B lies at 4 AU from the Sun.
How much more light does Planet A receive than Planet B?
4 divide 2 = 2
22 = 4
Answer = 4 times
Question 2
Venus orbits the Sun at 108 million km.
Mars orbits the Sun at 226 million km.
How much more light does Venus receive from the Sun than Mars?
1082 = 11664
2262 = 51076
51076 divide 11664 = 4.37 times
Question 3
Two asteroids revolve around a common centre of gravity. They are of Masses 4M and 7M. They are 3 distances apart.
What is their gravitational pull?
4M x 7M
3d x 3d
=
28M
9d
= Gravitational Pull of 3.1
Interactive
Summary
Newton's law of universal gravitation
| F = G | m1m2 r2 |
F is the force between the masses
G is the gravitational constant (6.674×10-11 N·kg–2·m2
m1 is the first mass
m2 is the second mass
r is the distance between the centres of the masses
Animation
Links
- PhET Interactive Simulations Gravity & Orbits
- HyperPhysics, Georgia State University Explaining the Inverse Square Law
- Exploratorium Experiment you can do
- Solar Views Educator's Guide to The Inverse Square Law

 | © All Rights Reserved |
| © All Rights Reserved |